The reason it is an interesting question is that relativistic physics is based on Minkowski space (or distorted versions) and the most fundamental symmetry of this is conformal symmetry.
The answer is a combination of:
- translations
- scales
- rotations
- boosts
- inversions (which invert the distance metric (positive or negative), so flip around the double hyperboloid in the time-like region and around the hyperboloid of revolution in the space-like region).
However, this isn't totally useful as it doesn't give a clear image of your average conformal transformation. For comparison, we can define any arbitrary conformal transformation of 3d Euclidean space as:
An arbitrary rotation around an arbitrary circle in space.
This covers all cases, sometimes in degenerate form, for example an ordinary rotation is when the circle has infinite radius, an ordinary translation is the limit as the radius increases, the circle becomes farther away and the rotation around it decreases.
The equivalent definition for 3+1 Minkowski space can be described in two ways, in terms of linear operations (e.g. rotations, boosts) or in terms of curvature. In both cases the transform is described in the time-like region when it involves a time flip, and in the space-like region when it involves a space flip:
Linear
Space-like:
An arbitrary rotation around an arbitrary circle in space, with equal and opposite arbitrary boosts through the circle at two times around an arbitrary point in time.
Time-like:
An arbitrary boost through an arbitrary sphere in space at an arbitrary point in time.
Curvilinear
Space-like:
An arbitrary cupping (positive curvature) of space together with an arbitrary (boost) acceleration through the axis of the bulge.
Time-like:
An arbitrary radial expansion/contraction at an arbitrary point in space and time.
I'm still not sure if this covers all combinations of transforms but it seems close at least. It is a nice and simple generalisation of 'rotation around a circle' for space-like regions and 'boost through a plane' for time-like regions.







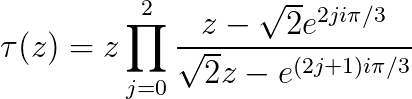.png)













